wiki
AVL 树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为一,所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下都是O(log n)。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。
图解
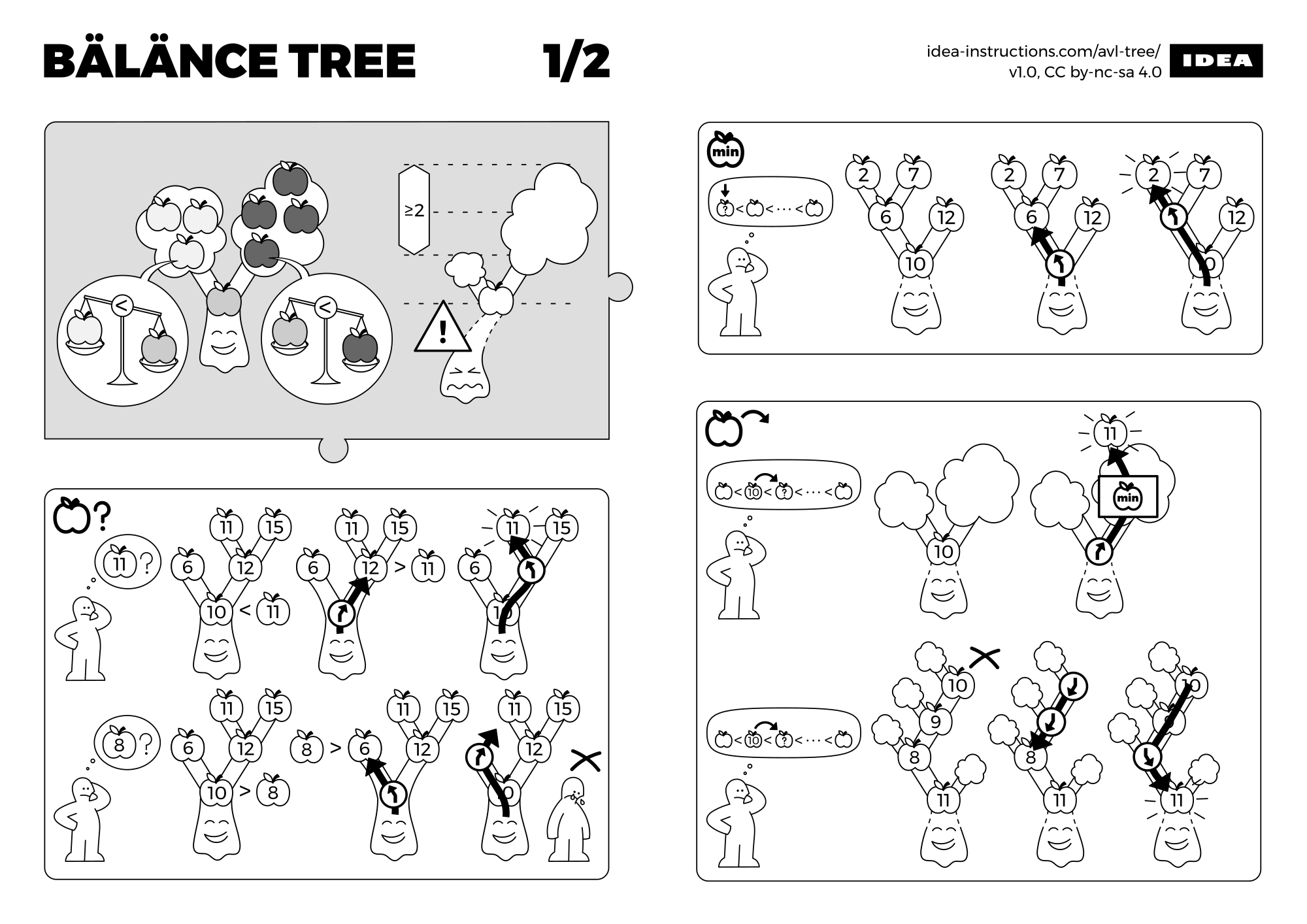
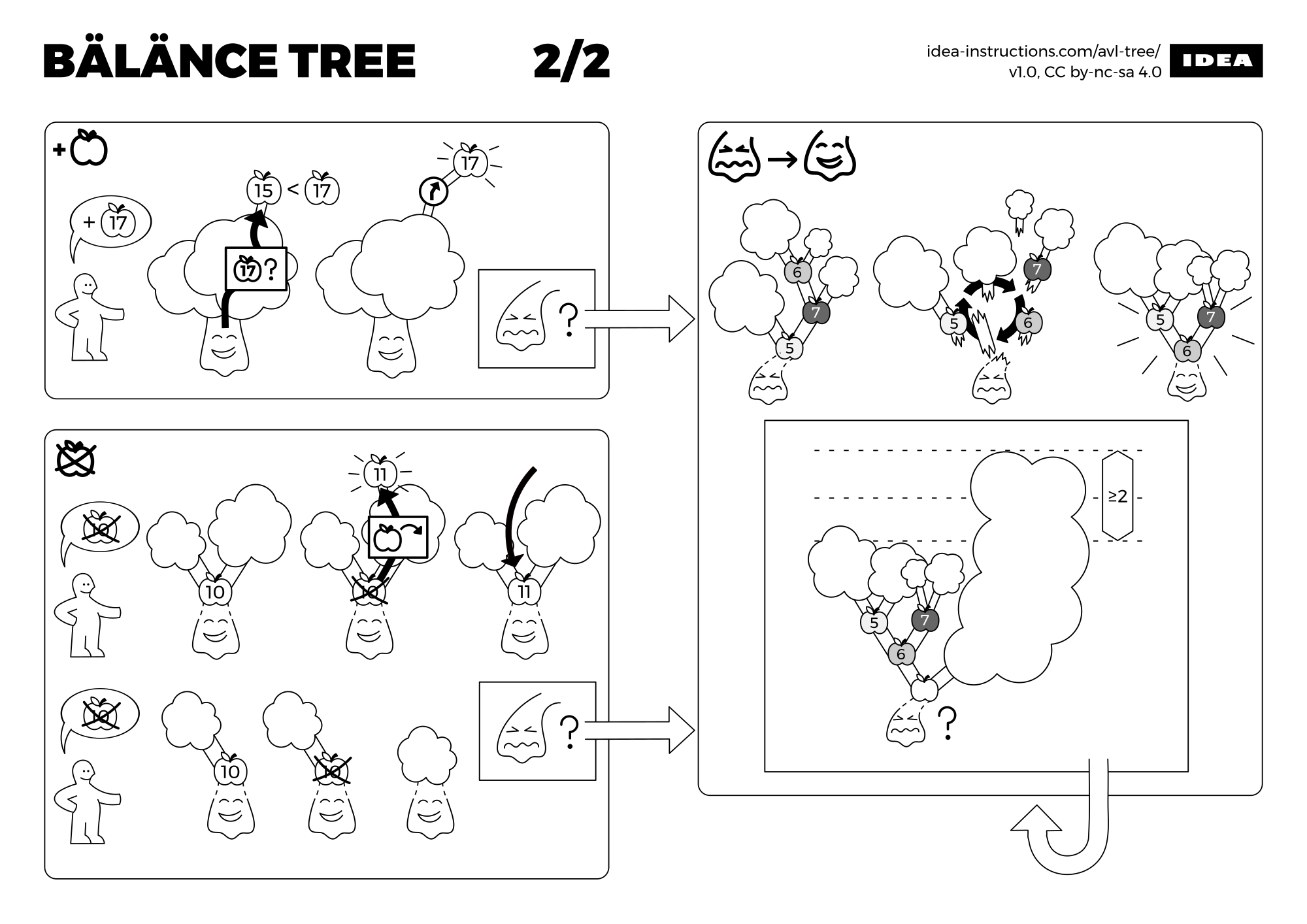
步骤:
- 左节点比父节点小,而父节点比右节点小。如果根节点左右子树的高度差超过1,则变得不平衡
- 树是否含元素11?11比10大,则查找10的右子节点为12;11比12小,则查找12的左子节点为11。同样,树是否含元素8?8比10小,则查找10的左子节点为6;8比6大,则查找6的右子节点,其不存在,即树是不含元素8
- 寻找树的最小元素?从根节点出发,一直寻找左子节点,最后一个叶子节点就是树中最小元素
- 寻找元素10的下一个元素?若根节点为10,则从10的右子树中查找最小元素。若根节点不是10,则先找到元素10,其若没有右节点,则一直寻找父节点,直到直到比10大的元素为止
- 在树中插入17或删除10,破坏了树的平衡,这时候需要通过旋转恢复树的平衡
