读书笔记

线性代数的本质-3Blue1Brown

1. 向量究竟是什么

TODO

2. 线性组合、张成空间与基

TODO

3. 矩阵与线性变换

3.1. 词汇

  • Linear transformations：线性变换

3.2. 线性：变换后

直线仍是直线；
原点保持固定；

3.3. 线性变换一个重要推论

一个向量是 i-hat 与 j-hat 的特定线性组合，变换后仍为 i-hat 与 j-hat 同样的线性组合，即你可以只通过变换后的 i-hat 与 j-hat，直接推论出变换后的该向量

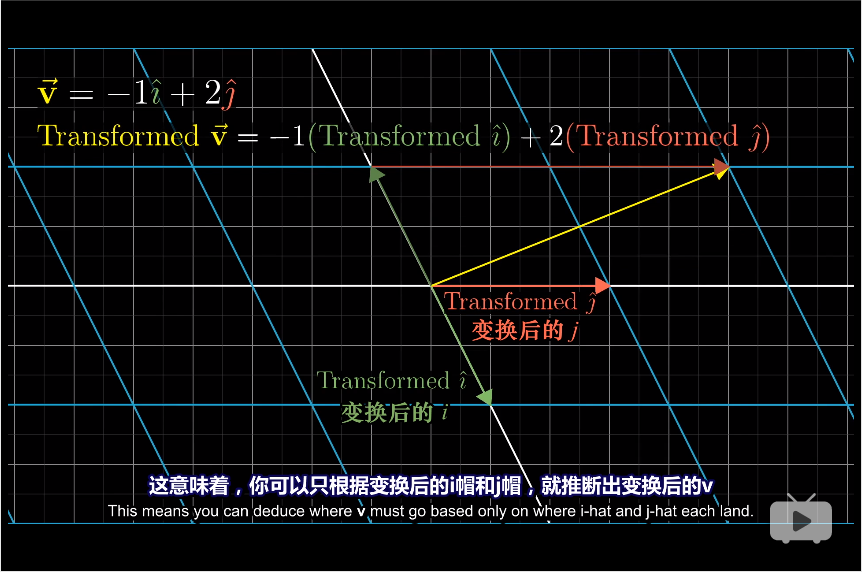
线性变换-1

3.4. 2×2矩阵

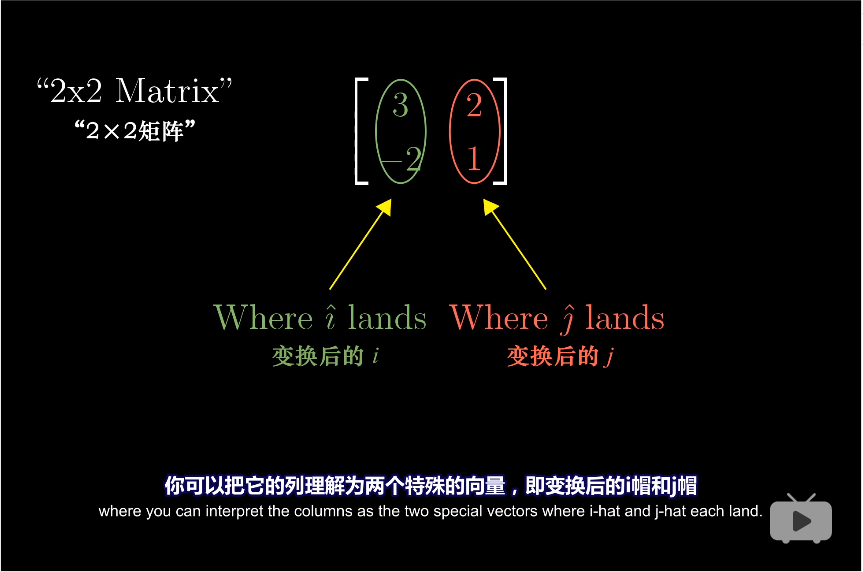
一个二维线性变换仅由四个数字就可完全确定，我们通常把这些坐标包装在2×2格子中，称为2×2矩阵。

如果你有一个给定向量以及一个描述现象变换的2×2矩阵，你想了解这个线性变换对该向量的影响，你只需要取出向量的坐标将它们与矩阵特定列相乘，再将它们的积求和即可。

线性变换-2

4. 矩阵乘法与线性变换复合

TODO

附注1

TODO

5. 行列式

5.1. 词汇

  • Parallelepiped：平行六面体
  • Generally stretches space：向外拉伸空间
  • Generally squishes space：向内挤压空间
  • determinant：行列式
  • orientation：定向，取向

5.2. 行列式的概念

线性变换改变的比例被称为这个变换的行列式(The determinant of a transformation)。

5.3. n阶行列式

  • 二阶行列式可看做平行四边形的面积，正负号表示取向
  • 三阶行列式可简单看做平行六面体的体积，正负号可用右手定则判断
  • 行列式为0，矩阵必然线性相关

5.4. 集合概念

ad 表示矩形面积，bc表示矩形在对角线方向的挤压量（拉伸量）。

行列式

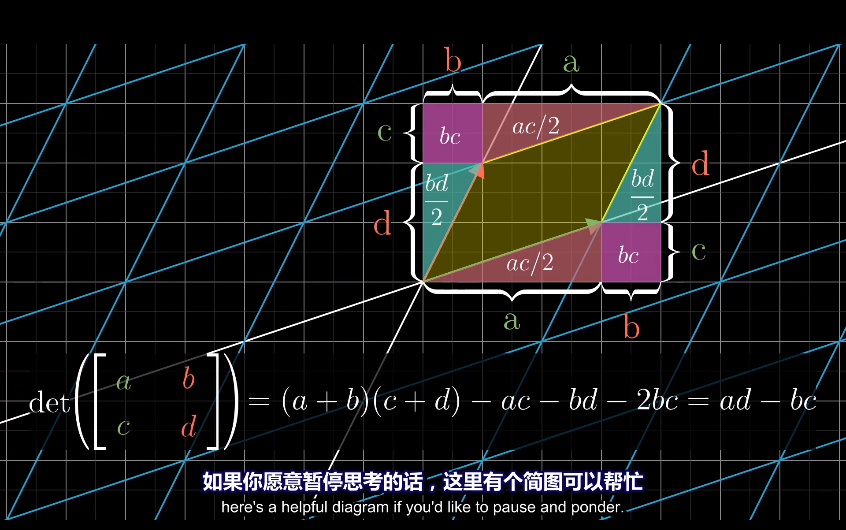
6. 逆矩阵、列空间、零空间

6.1. 词汇

  • Inverse matrices：逆矩阵
  • Column space：列空间
  • Rank：秩
  • Null space：零空间
  • Gaussian elimination：高斯消元法
  • Row echelon form：行阶梯型
  • Linear system of equations：线性方程组

6.2. Ax=v

求解Ax=v，意味着寻找一个向量x，使它变换后与v重合。

6.3. 矩阵相乘

A与A的逆矩阵相乘，等于一组基向量。

逆矩阵

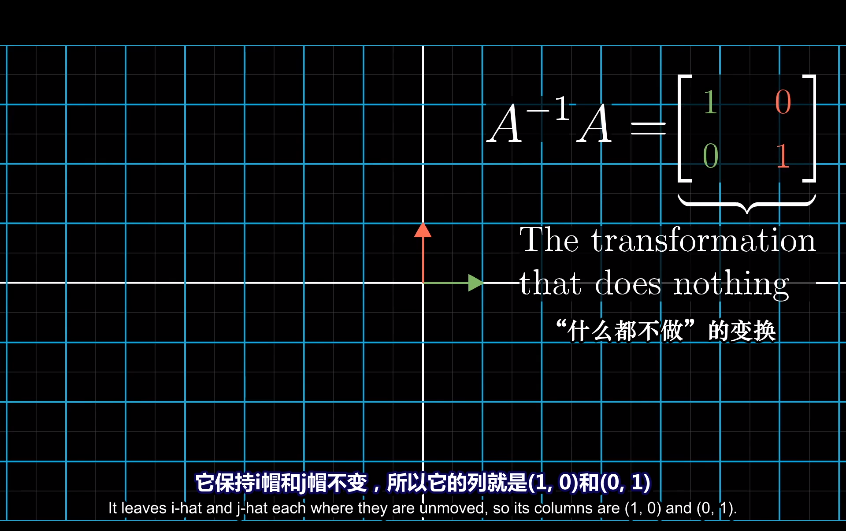
6.4. 变换

只要变换A，不会将空间压缩到一个更低的维度时，即det(A)不等于0，就必然存在A的逆矩阵，因为你无法将一条直线“解压缩”为一个平面。

6.5. 秩

秩表示压缩后的空间维数。

6.6. 列空间

所有可能的输出向量Av构成的集合叫做矩阵A的列空间。

6.7. 满秩

秩与列数相等称为满秩。

6.8. 零空间

变换后落在原点的向量集合成为零空间。

附注2 非方阵

  • 变换后为3×2矩阵，三维空间用2个三维坐标表示，即为三维空间的一个平面上
  • 变换后为2×3矩阵，三维空间用3个二维坐标表示，即为二维空间
  • 变换后为1×1矩阵，一维空间用1个一维坐标表示，即为数轴上点

7.点积与对偶性

7.1. 词汇

  • Dot product：点积
  • Duality：对偶性

7.2. 点积

点积就是矩阵向量的乘积。两个向量点乘就是将其中一个向量转换为线性变换。

线性变换推论可知，变换后的该向量可以从变换后的i-hat与j-hat得到，而两者的变换又与投影有关，所以点积与投影自然而然联系起来了。

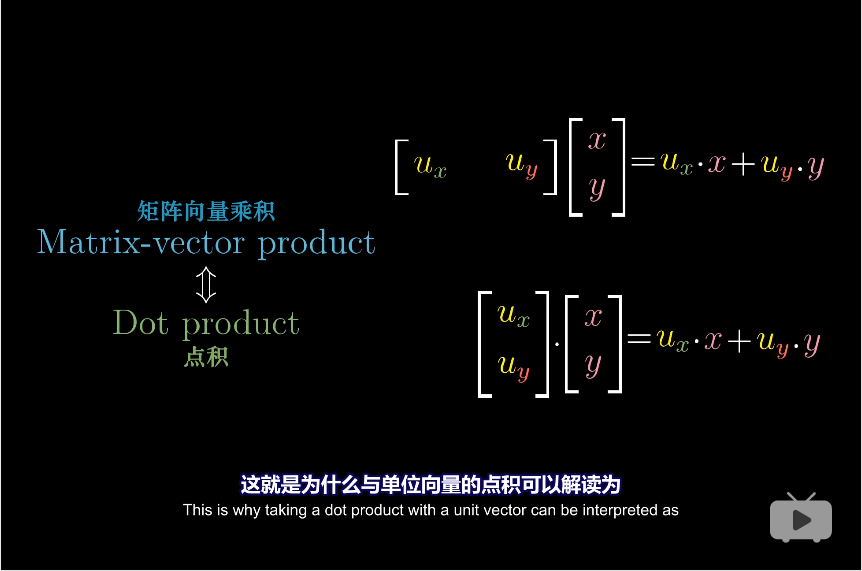
点积与对偶性

7.3. 向量

向量不仅仅是空间的一个箭头，更该把它看成线性变换的载体。向量仿佛一个特定变换的概念性记号，有时，想象空间中的向量比想象整个空间移动到数轴上更加容易理解。

7.4. 严格的线性性质

L(v+w) = Lv+Lw：可加性
L(cv) = cLv：成比性（一阶齐次）

8.叉积的标准介绍

8.1. 词汇

  • Cross product：叉积

8.2. 概念

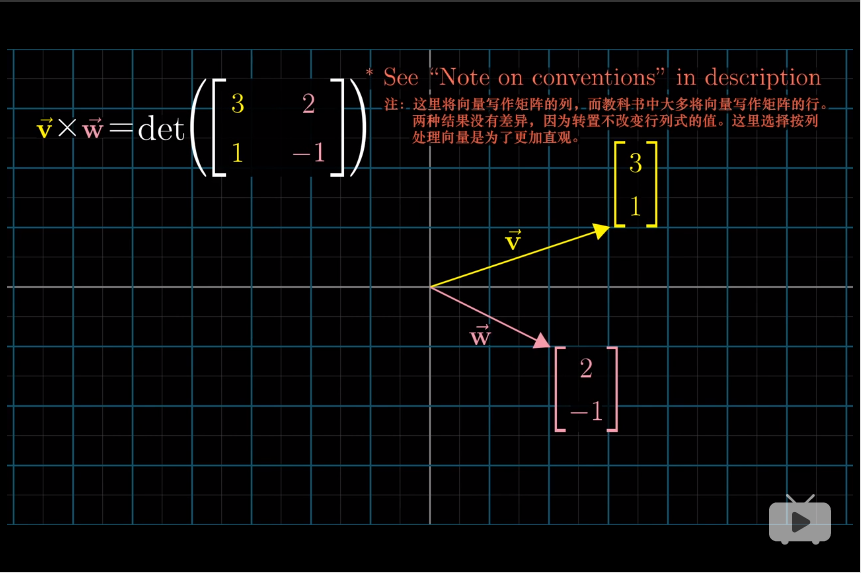
两向量的叉积就是两者形成的平行四边形的面积，方向利用右手定则判断。通常用来度量面积变换比例的行列式，给出了平行四边形的面积。

严格意义上的叉积是使用2个三维向量生成1个新的三维向量。

叉积所生成的对偶向量，必然与输入的两个向量垂直，并且长度数值上等于输入的两个向量的张成的平行四边形。

叉积

9.基变换

9.1. 坐标系

发生在向量与一组数之间的任意转化，都称作一个坐标系。

9.2. 向量新理解

我们在线性变换前所想的向量是我们的基向量的一种特定的线性组合，而线性变换的一个重要特征(第3章的线性变换推论)就是，变化后的向量仍然是相同的线性组合，不过使用的是新的基向量。

基变换-1

基变换-2

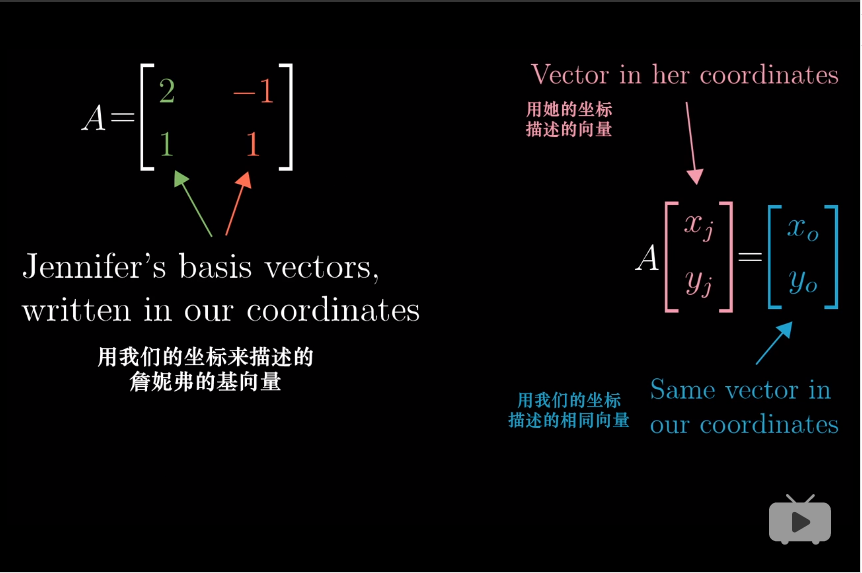
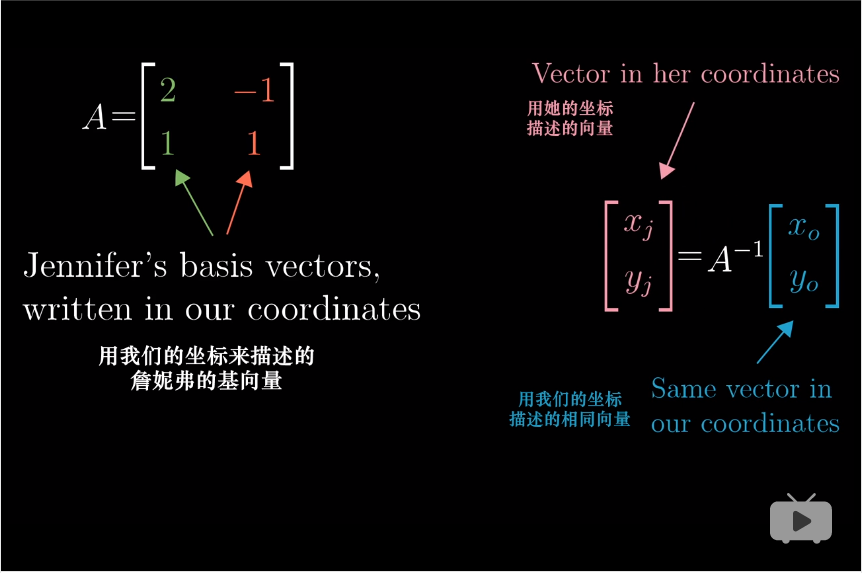
9.3. 转换一个矩阵

如何转换一个矩阵，即用她的坐标来表示一个与你相同的变换：

  1. 从詹妮弗的语言描述的任一向量出发
    基变换-3
  2. 利用基变换转化为我们的语言描述
    基变换-4
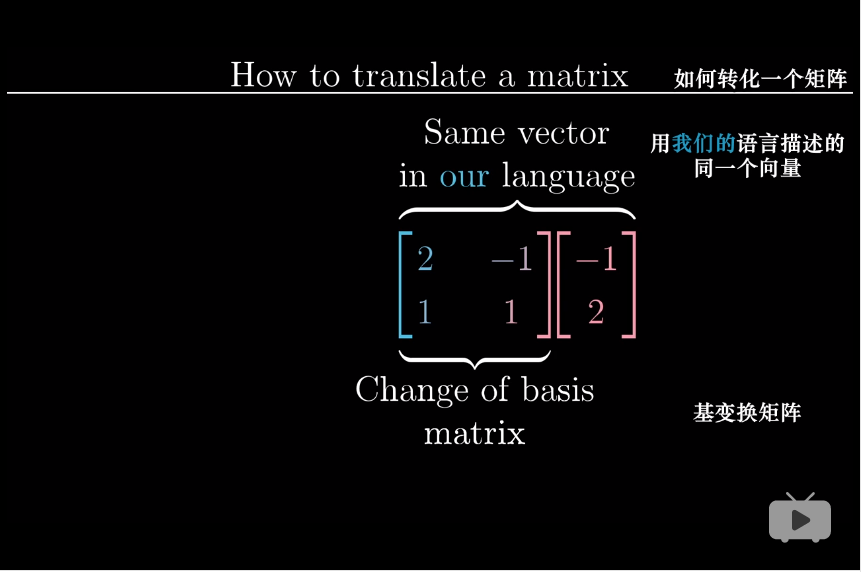
  3. 所得结果左乘线性变换矩阵([0,1],[-1,0]为你的变换矩阵，即旋转逆时针90°)
    基变换-5
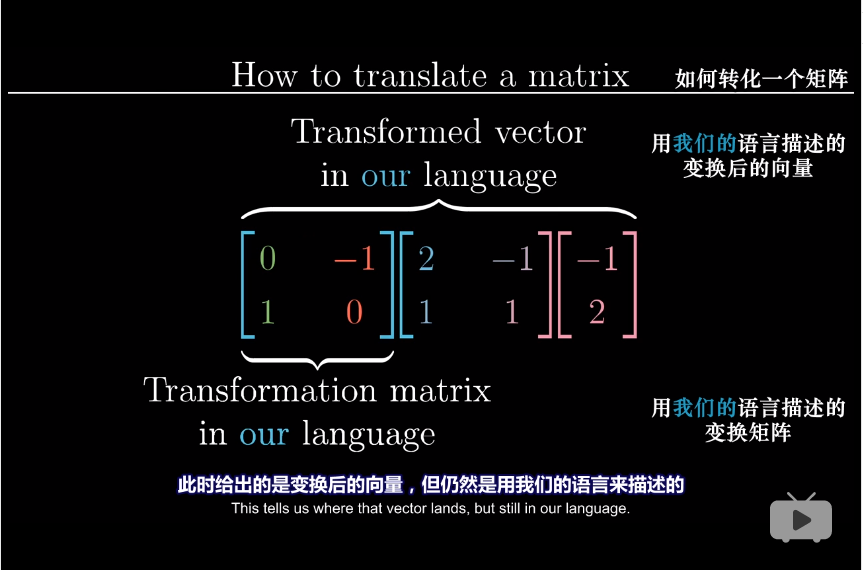
  4. 再将结果左乘基变换的逆矩阵
    基变换-6
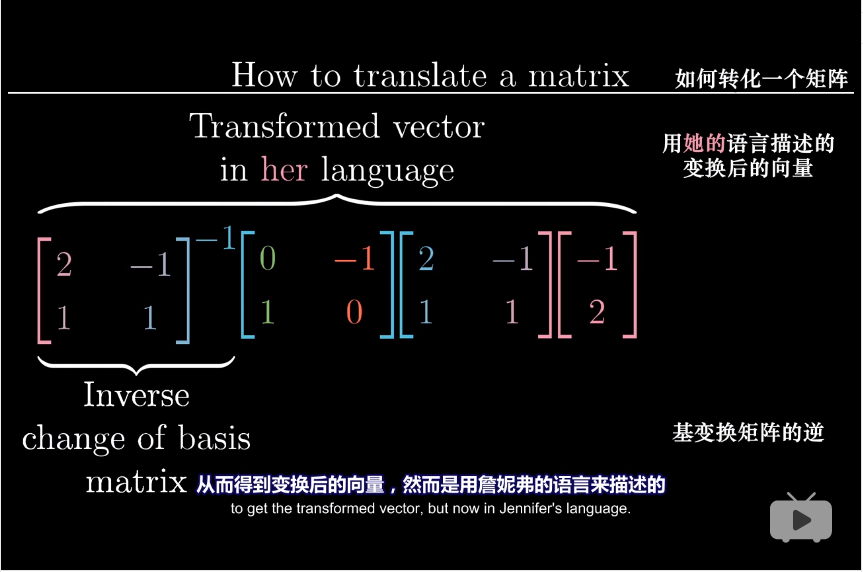
  5. 这三个符合矩阵就是用她的语言来描述一个与你相同的线性变换，它接收詹妮弗语言描述的向量，并输出她的语言描述的变换后的向量
    基变换-7

9.4. A-1MA

表达式 A-1MA 暗示一种数学上的转移作用，中间M矩阵代表你所见的变换，两侧的矩阵代表转移作用，也就是视角的转换，矩阵乘积仍然代表同一个变换，只不过是从其他的人角度来看。

10.特征向量与特征值

10.1. 词汇

  • Eigenvectors：特征向量
  • Eigenvalues：特征值
  • Diagonal matrix：对角矩阵
  • Eigenbasis：特征值

10.2. 特征向量

特征向量指变换后仍留在其张成空间内的向量；每个特征向量都有一个所属的特征值，被称为特征值，即衡量特征向量在变换中拉伸或压缩比例的因子。

11.抽象向量空间

11.1. 词汇

  • linear operators：线性算子
  • Axioms：公理

11.2. 向量加法和数乘规则

抽象向量空间