wiki
本章知识点会涉及考试中的各种题型,约占 4 分。本小时的内容偏重于理论
1. 算法的基本概念
1. 基本概念
算法(Algorithm)是对特定问题求解步骤的一种描述,它是指令的有限序列,其中每一条指令表示一个或多个操作。
2. 算法的特性
有穷性、确定性、可行性、输入、输出。
3. “好”算法的要求
正确性、健壮性、高效性。
4. 算法的表示
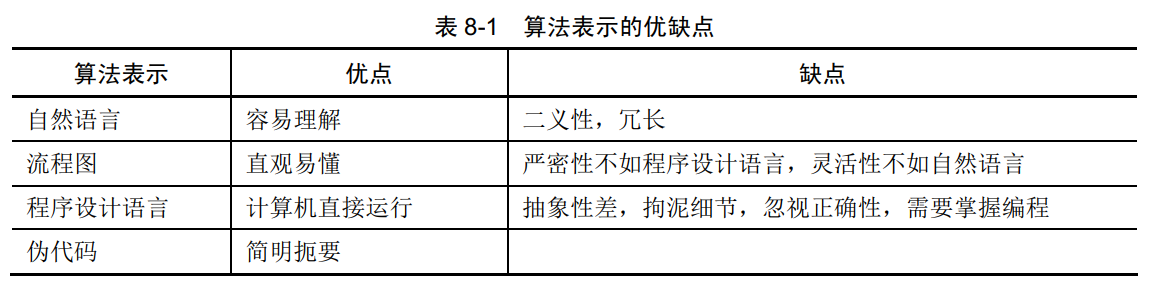
2 算法的分析基础
1. 算法复杂性
时间复杂性、空间复杂性。
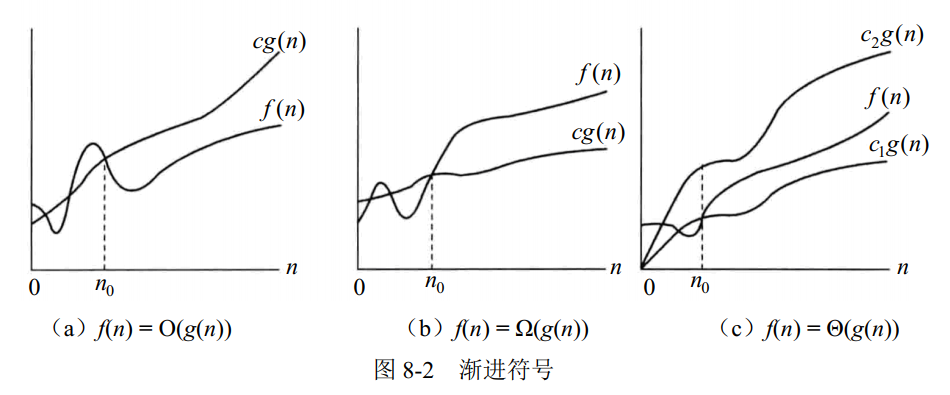
2. 渐进符号
1. O 记号
给出一个函数的渐进上界。给定一个函数 g(n),O(g(n)) 表示为一个函数集合 {f(n):存在正常数 c 和 n0,使得对所有的 n≥n0,有 0≤f(n)≤cg(n)}。
2. Ω 记号
给出一个函数的渐进下界。给定一个函数 g(n),Ω(g(n))表示为一个函数集合 {f(n):存在正常数 c 和 n0,使得对所有的 n≥n0,有 0≤cg(n)≤f(n)}。
3. Θ 记号
给出一个函数的渐进上界和下界,即渐进确界。给定一个函数 g(n),Θ(g(n))表示为一个函数集合 {f(n):存在正常数 C1、C2 和 n0,使得对所有的 n≥n0,有 0≤C1g(n)≤f(n)≤C2g(n)}。
3. 递归式
从算法结构上看,算法分为递归式和非递归式。递归算法的时间复杂度分析方法有如下几种:
- 展开法:将递归式中等式左右两边的项根据递归式进行替换,称为展开。展开后的项再次展开,如此下去,直到得到一个求和表达式。
- 代换法:当归纳假设用最小值时,用所猜测的值代替函数的解。有 3 个步骤:猜测解的形式、数学归纳法证明猜测、求出使解有效的常数。
- 递归树法:弥补代换法猜测困难的缺点,每一个结点都代表一个子集合代价,将树中每一层结点相加得到每一层代价,再将每一层相加得到总代价。
- 主方法:也叫主定理法,给出了形如 T(n)=aT(n/b)+f(n) 的快速方法。
3. 分治法
1. 递归的概念
递归是指子程序直接或者间接调用自己。
递归的两个基本要素:终止条件、递归体。
2. 分治法思想
分解、求解、合并。
3. 实例
归并排序。
4. 动态规划
类似分治法,与它不同的是,动态规划分解得到的子问题不是独立的,为避免计算多次,可以使用一个表来记录已解决的子问题。
1. 动态规划基本思想
- 找出最优解的性质,并刻画其结构特征
- 递归定义最优解的值
- 自底向上算出最优解
- 构造最优解
可以使用动态规划解决的的问题,有如下 2 个性质:
- 最优子结构:如果一个问题的最优解中包含了其子问题的最优解,就说该问题有最优子结构。
- 重叠子问题:解原问题的递归算法可反复解同样的子问题,而不是总在产生新的子问题。
2. 动态规划实例
0-1 背包问题。
5. 贪心法
1. 贪心法基本思想
用于解决最优解问题,类似动态规划,但仅在根据当前已有信息作出选择。换言之,贪心算法并不从整体最优考虑。
2. 贪心法实例
活动选择问题、背包问题
6. 回溯法
1. 解空间
问题的解空间至少包含问题一个最优解,并将解空间组织起来,方便回溯法搜索,一般表示为数或图形式。
2. 贪心法基本思想
确定了解空间的组织结构后,回溯法从根结点出发,以深度优先方式开始搜索解空间,成为活结点,当不能再向深处移动时,回溯到最近的一个活结点,直到所要求的解或者解空间无活结点为止。
3. 贪心法算法框架
递归和非递归两种方式。
4. 贪心法实例
0-1 背包问题。
7. 分支限界法
类似回溯法,但求解目标不同,其目标是找出满足约束条件的一个解,或找出是目标达到极大极小的解。
分支限界法以广度优先或最小耗费优先的方式搜索解空间。常用的有两种类型:
- 队列式(FIFO)分支限界法:将活结点组成队列,按照 FIFO 选择下一个结点作为扩展结点
- 优先队列式分支限界法:将活结点组成优先队列,并按照优先级选取下一个结点作为扩展结点
8. 概率算法
在执行某些步骤时,可以随机选择下一步如何进行,同时以允许结果出现较小的概率出现错误为代价,大幅减少算法时间。
概率算法有如下基本特征:
- 输入包括两部分,原问题输入、供算法进行随机选择的随机数序列
- 在运行过程中,包括随机选择,根据随机值决定运行路径
- 不保证结果一定正确,但能限制出错率
- 相同输出可能不同结果
有 4 种类型:
- 数值概率算法:常用于数值问题求解,近似解精度随时间增加而提高
- 蒙特·卡罗(Monte Carlo)算法:用于求解精确解,得到正确解的概率随时间增加而提高
- 拉斯维加斯(Las Vegas)算法:一旦找到解,一定是正确解,得到正确解的概率随时间增加而提高,求解次数足够多,求解失效率可以足够小
- 舍伍德(Sherwood)算法:在一个确定性算法的最坏情况下和平均情况下的计算复杂度有较大差别时,可在其中引入随机性,将它改造成舍伍德算法,消除最坏情形与特定实例的关联
9. 近似算法
近似算法基本思想是放弃最优解,采用近似最优解,以简化算法和降低时间复杂度。
1. 近似算法性能标准
- 算法的时间复杂度:时间负责度必须是多项式的,是近似算法的基本目标
- 解的近似程度
2. 近似算法实例
定点覆盖问题、TSP 问题、子集和数问题。
